How-to Easily Design an Adder Using VHDL

Preface
We are going to take a look at designing a simple unsigned adder circuit in VHDL through different coding styles. By doing so, this will get you familiar with designing by different methods and, hopefully, show you to look for the easy solution before attempting to code anything.

The specific circuit we are going to model in this how-to is a 4-bit unsigned adder. In the first pass of the design, we will build a 1-bit full adder (or (3,2) counter) slice that will be used to build the full 4-bit adder. In the second pass of the design, we are going to build the circuit using the IEEE std_logic unsigned package, a much more code efficient and scalable design.

This how-to assumes you have some knowledge of VHDL and understand concepts such as entities, architectures, and signals. If you need further VHDL language references, please check under the tutorials section of Student Resources. Let begin!

1-Bit Full Adder
As you know, a 1-bit full adder is characterized by the following equations:

sum = x xor y xor cin
cout = (x and y) or (x and cin) or (x and cout)

where x, y, and cin are the two inputs and the carry in, respectively while sum and cout are the sum and carry out. A pictorial representation of the component is listed in figure 1.

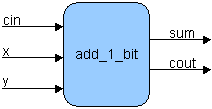
Figure 1 - 1-Bit Full Adder Component

The VHDL code for the above component (downloadable file add_1_bit.vhd) is as follows:

  library IEEE;
  use IEEE.std_logic_1164.all;

  entity add_1_bit is
    port (
      x: in std_logic;
      y: in std_logic;
      cin: in std_logic;
      sum: out std_logic;
      cout: out std_logic
    );
  end add_1_bit;

  architecture rtl of add_1_bit is
  begin
    sum <= x xor y xor cin;
    cout <= (x and y) or (x and cin) or (y and cin);
  end rtl;

As you can see, we are using the standard IEEE libraries, which include std_logic, in order to create components that can be synthesized easily to hardware. Using signal types such as bit may not synthesize or produce unpredictable results. Always use the std_logic_1164 library!

This is a pretty standard component. In the entity declaration, x, y, and cin are declared as inputs of type std_logic. The outputs are sum and cout of type std_logic. In the architecture section, we define the outputs sum and cout to be concurrent statements based directly off the inputs. Nothing special about this component, I'm sure you have already seen a version of this model.

4-Bit Unsigned Adder using 1-Bit Full Adder Component
Now we are going to make four copies of the above component to make our 4-bit unsigned adder component, thus producing a ripple-carry adder. This is done through instantiating four copies of the above 1-bit adder component in VHDL. Figure 2 illustrates the connections of this component.

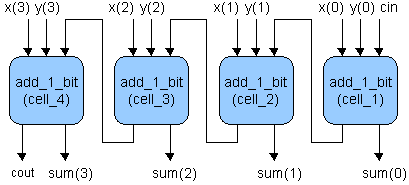
Figure 2 - 4-Bit Unsigned Adder

The inputs to the component are the 4-bit unsigned numbers, x and y, and the carry in that includes cin and the internal ripple carries between each 1-bit block. The 4-bit output sum and cout are shown as outputs of the systems. Listed below is the VHDL code for the component (downloadable add_4_bits.vhd).

  library IEEE;
  use IEEE.std_logic_1164.all;

  entity add_4_bits is
    port (
      x: in std_logic_vector(3 downto 0);
      y: in std_logic_vector(3 downto 0);
      cin: in std_logic;
      sum: out std_logic_vector(3 downto 0);
      cout: out std_logic
    );
  end add_4_bits;

  architecture rtl of add_4_bits is
    component add_1_bit
      port (
        x: in std_logic;
        y: in std_logic;
        cin: in std_logic;
        sum: out std_logic;
        cout: out std_logic
      );
    end component;

    signal i_carry: std_logic_vector(2 downto 0);
  begin
    cell_1: add_1_bit
      port map (x(0), y(0), cin, sum(0), i_carry(0));

    cell_2: add_1_bit
      port map (x(1), y(1), i_carry(0), sum(1), i_carry(1));

    cell_3: add_1_bit
      port map (x(2), y(2), i_carry(1), sum(2), i_carry(2));

    cell_4: add_1_bit
      port map (x(3), y(3), i_carry(2), sum(3), cout);
  end rtl;

You can see that we define the component add_1_bit in the architecture declaration section of the code. Please also notice that this declaration follows VHDL-87 format and NOT the '93 version. This is because the synopsis synthesis tool is VHDL-87 compliant and we need to code to those rules in order to generate valid synthesis results. Coding in '93 will not (currently) work.

Four versions of this component are then declared in the body section of the code, with all of the appropriate "glue" between each component. As this point, you must be asking, "isn't there an easy way to do this?". From my perspective, this is alot of code for just a 4-bit unsigned adder; the point to VHDL is to make it easier to perform operations such as the above. Let's take alook at an easier way.

4-Bit Unsigned Adder Using std_logic_unsigned
Using the same entity as above, look at the code below and notice how much and where it has been shortened (downloadable add.vhd).

  library IEEE;
  use IEEE.std_logic_1164.all;
  use IEEE.std_logic_unsigned.all;

  entity add is
    generic (width: integer:=4);
    port (
      x: in std_logic_vector((width-1) downto 0);
      y: in std_logic_vector((width-1) downto 0);
      cin: in std_logic;
      sum: out std_logic_vector((width - 1) downto 0);
      cout: out std_logic
    );
  end add;

  architecture rtl of add is
    signal i_sum: std_logic_vector(width downto 0);
    constant i_cin_ext: std_logic_vector(width downto 1) := (others => '0');
  begin
    i_sum <= ('0' & x) + ('0' & y) + (i_cin_ext & cin);
    sum <= i_sum((width-1) downto 0);
    cout <= i_sum(width);
  end rtl;

The first thing you will notice, at the top of the code, is the reference to the std_logic_unsigned package, used for unsigned std_logic arithmetic operations. This package contains a procedure called "+" which we use as an addition within the body of the architecture. This "+" takes three unsigned std_logic_vectors and adds them, returning a result.

The other should be the use of a generic. A generic lets us produce code that can be changed by the passed parameter. In our case, we let the generic width be the bit width of the two numerands, thus making the code scalable to any width of signals.

For this specific example, we take x and y, concatenate a '0' to the beginning (unsigned logic). For cin, we concatenate a vector one less than the generic constant. These are all added with "+" and assigned to the result i_sum. We then split i_sum into the sum and the carry out. This can be done a number of ways but this is one of them and, as you can see, is much simpler than the previous example. Additionally, with the use the generic width, the component becomes much more reusable, a quality always desired by designers.

I have found that the performance of such code to be better, while easier to code, than other algorithmic techniques. This is probably due to the fact that the synthesis tools will understand what is inferred by the IEEE libraries more than any algorithm you can write. However, be careful of the cin vector. Good synthesis tools will recognize that the cin vector is really only cin padded with zeros, and thus will apply only the cin signal to the input of the cin portion of the fast carry logic for the FPGA. However, others will not; check the output of the synthesis tool to make sure that the fast carry logic was used on the FPGA (assuming such logic exists). Of course performing hand layout methods or using LogicBLOX will produce smaller, faster results. But those methods become technology dependent (i.e. tied to your target device) while this code will not.

fouldsbr@msu.edu